GEMV Tutorial 5: Multiple PEs¶

The power of the Wafer-Scale Engine lies in its hundreds of thousands of processing elements. Now that we’ve covered some basics for writing a complete program using a single PE, let’s create our first program using multiple PEs.

Learning objectives¶

After completing this tutorial, you should know how to:

Define a layout file that compiles code for multiple PEs
Copy data to and from multiple PEs on the device

Example overview¶

Our program will now run on four processing elements (PE). We will demonstrate the program with a simulated fabric consisting of an 11 x 3 block of PEs.

For this program, each PE will perform the exact same work; that is, we will copy A, x, and b to each of the four PEs, the four PEs will each perform a GEMV, and then we will copy back the result y from each PE.

pe_program.csl does not change. We simply need to modify layout.csl to assign it to multiple PEs. We also need to modify our host code to copy to and from multiple PEs instead of just one.

Problem Steps¶

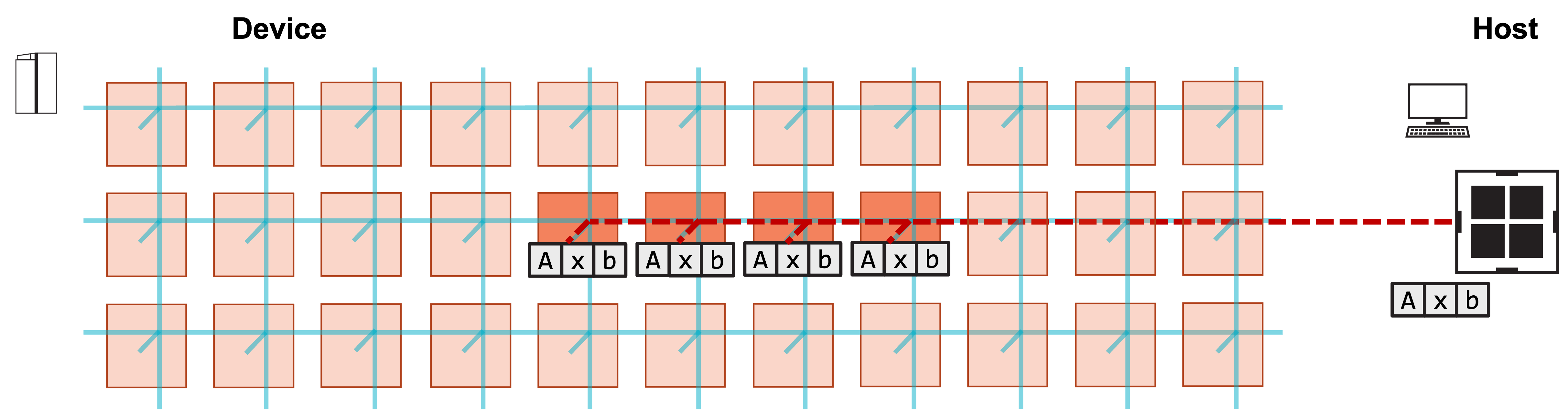
Visually, this program consists of the following steps:

1. Host copies A, x, b to four PEs on device.

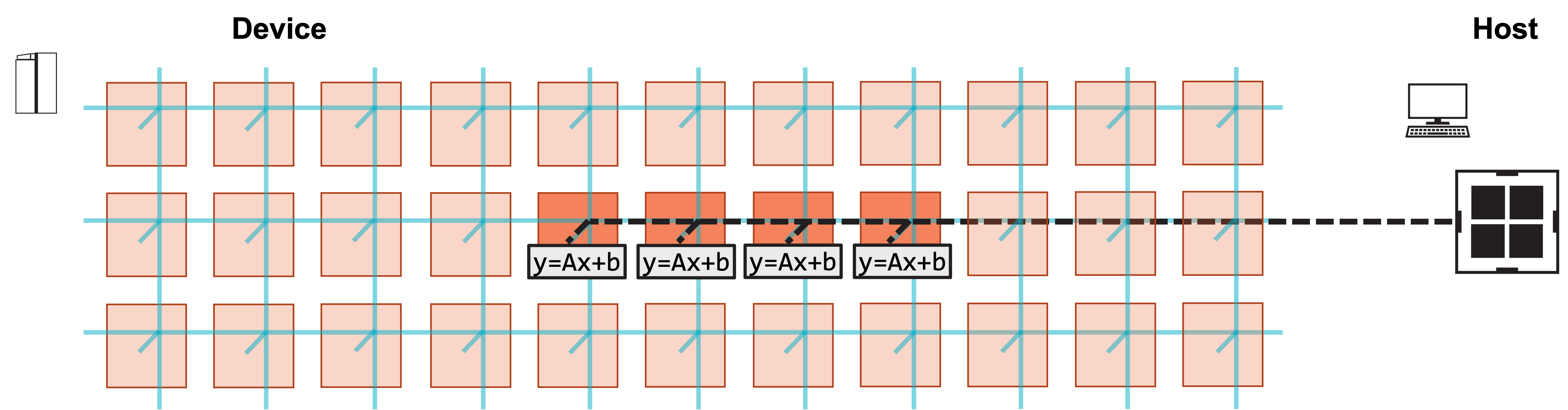
2. Host launches function on each PE to compute y.

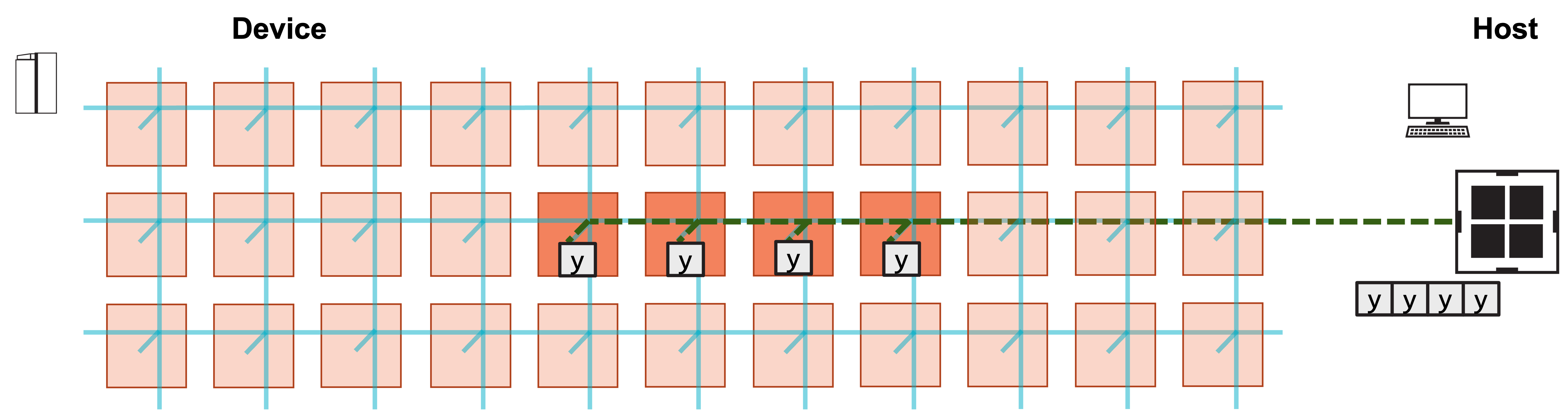
3. Host copies result y from each PE.

Modifying the CSL¶

How do we need to modify our layout file to support running the program on multiple PEs?

We need to modify @set_rectangle to reflect our new program rectangle.
We need to modify our memcpy infrastructure to reflect the use of multiple PEs.
We need to call @set_tile_code for each coordinate inside this program rectangle.

pe_program.csl remains largely the same; we simply assign it to more PEs. We include the new layout.csl below, and highlight the changes.

// matrix dimensions on each PE
param M: i16;
param N: i16;

// number of PEs in program
param width: i16;

const LAUNCH: color = @get_color(8);

const memcpy = @import_module("<memcpy/get_params>", .{
  .width = width,
  .height = 1,
  .LAUNCH = LAUNCH
});

layout {
  // PE coordinates are (column, row)
  @set_rectangle(width, 1);
  for (@range(i16, width)) |x| {
    @set_tile_code(x, 0, "pe_program.csl", .{
      .memcpy_params = memcpy.get_params(x),
      .M = M,
      .N = N
    });
  }

  // export symbol names
  @export_name("A", [*]f32, true);
  @export_name("x", [*]f32, true);
  @export_name("b", [*]f32, true);
  @export_name("y", [*]f32, false);
  @export_name("compute", fn()void);
}

Notice that we define a new compile time parameter width, whose value will be set in our compile command. We will use this value to set the number of PEs in our row of PEs used by the program.

When we import <memcpy_multi/get_params>, we use width to specify the width of the program rectangle for which memcpy infrastructure will be generated. The height is still 1.

Inside of our layout block, our program rectangle is now specified with @set_rectangle(width, 1). For each of the PEs in this rectangle, we must call @set_tile_code, so we do this in a loop. The loop coordinate is the PE’s x-coordinate, or column number, which is needed to set the correct memcpy_params for each PE.

Modifying the host code¶

Our host code must now copy A, x and b to multiple PEs, and must copy back y from multiple PEs. Let’s take a look at how we must modify our memcpy_h2d and memcpy_d2h calls in run.py to do this:

#!/usr/bin/env cs_python

import argparse
import json
import numpy as np

from cerebras.sdk.runtime.sdkruntimepybind import SdkRuntime, MemcpyDataType, MemcpyOrder # pylint: disable=no-name-in-module

# Read arguments
parser = argparse.ArgumentParser()
parser.add_argument('--name', help="the test compile output dir")
parser.add_argument('--cmaddr', help="IP:port for CS system")
args = parser.parse_args()

# Get matrix dimensions from compile metadata
with open(f"{args.name}/out.json", encoding='utf-8') as json_file:
  compile_data = json.load(json_file)

# Matrix dimensions
N = int(compile_data['params']['N'])
M = int(compile_data['params']['M'])

# Number of PEs in program
width = int(compile_data['params']['width'])

# Construct A, x, b
A = np.arange(M*N, dtype=np.float32)
x = np.full(shape=N, fill_value=1.0, dtype=np.float32)
b = np.full(shape=M, fill_value=2.0, dtype=np.float32)

# Calculate expected y
y_expected = A.reshape(M,N)@x + b

# Construct a runner using SdkRuntime
runner = SdkRuntime(args.name, cmaddr=args.cmaddr)

# Get symbols for A, x, b, y on device
A_symbol = runner.get_id('A')
x_symbol = runner.get_id('x')
b_symbol = runner.get_id('b')
y_symbol = runner.get_id('y')

# Load and run the program
runner.load()
runner.run()

# Copy A, x, b to device
runner.memcpy_h2d(A_symbol, np.tile(A, width), 0, 0, width, 1, M*N, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)
runner.memcpy_h2d(x_symbol, np.tile(x, width), 0, 0, width, 1, N, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)
runner.memcpy_h2d(b_symbol, np.tile(b, width), 0, 0, width, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

# Launch the init_and_compute function on device
runner.launch('compute', nonblock=False)

# Copy y back from device
y_result = np.zeros([M*width], dtype=np.float32)
runner.memcpy_d2h(y_result, y_symbol, 0, 0, width, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

# Stop the program
runner.stop()

# Ensure that the result matches our expectation
np.testing.assert_allclose(y_result, np.tile(y_expected, width), atol=0.01, rtol=0)
print("SUCCESS!")

First, note that we read one more parameter from the compile output, width. Our host code uses this to specify how many PEs it must copy tensors to and from.

Now let’s take a closer at the mempcy_h2d calls:

runner.memcpy_h2d(A_symbol, np.tile(A, width), 0, 0, width, 1, M*N, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)
runner.memcpy_h2d(x_symbol, np.tile(x, width), 0, 0, width, 1, N, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)
runner.memcpy_h2d(b_symbol, np.tile(b, width), 0, 0, width, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

We want to copy each of A, x, and b to each PE in our program rectangle. But memcpy_h2d does not perform a broadcast; it takes its input array and distributes it within the region of interest (ROI) based on the order parameter. Here, we use np.tile to duplicate each array width times.

In the first memcpy_h2d, the input array np.tile(A, width) is a 1D array formed by duplicating A width times, so the full input array’s size is M*N*width. Our ROI is specified by 0, 0, width, 1, meaning that we copy to the a row of width PEs beginning at PE (0, 0). We copy M*N elements to each PE.

Because our order is ROW_MAJOR, the result is that PE (0, 0) will receive the first M*N elements of the tiled array, PE (1, 0) will receive the next M*N elements, and so on. Thus, each PE will receive an identical M*N elements corresponding to a copy of A.

When we copy y back from the device, memcpy_d2h proceeds similarly:

y_result = np.zeros([M*width], dtype=np.float32)
runner.memcpy_d2h(y_result, y_symbol, 0, 0, width, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

Our output array y_result has size M*width, since each of the width PEs copies back the M elements of y.

We test that our copied-back result is correct for all PEs by comparing y_result to a tiled y_expected. See GEMV Tutorial 1: A Complete Program for an explanation of the remaining arguments.

Compiling and running the program¶

We add one additional compile time parameter to specify the width of our program rectangle:

$ cslc layout.csl --fabric-dims=11,3 --fabric-offsets=4,1 --params=M:4,N:6,width:4 --memcpy --channels=1 -o out
$ cs_python run.py --name out

We use the same command to run. You should see a SUCCESS! message at the end of execution.

Exercises¶

In this program, each PE is computing an identical GEMV. Modify the program so that each PE receives different values for the input tensors A, x, and b, and check that the computed outputs y are correct.

Next¶

Now that we’ve introduced multiple PEs into our program, instead of duplicating our GEMV problem between them, let’s actually distribute the work for computing a single GEMV.

SDK Documentation (1.0.0)

GEMV Tutorial 5: Multiple PEs

Contents